Massively Parallel Computers
The von Neumann architecture – the single processor computer – is past. The future belongs to custom and massively parallel computers, like General Purpose Graphical Processing Units (GPGPUs). Large amounts of data are channeled into the device, and thousands of small processors each work independently on a small portion of data, much like leaf-cutter ants devouring a plant.
My education has been centrally focused on collecting the knowledge to architect these processors. The smaller the components, the more ants can fit in the colony. The faster data is fed to the ants, and the closer it is, the faster the processing will be. These are the goals I pursue.
Research Interests
[expand title=”Computational Arithmetic” expanded=”true”]
Computational Arithmetic is the mathematics that defines the logic of the gates that compose a computer. People who actually design the computers study VLSI and know how to size and layout the transistors and design the vast circuitry that goes into developing a computer. People in Computational Arithmetic focus’ on a subset, on only the portion that calculates, trying to optimize the math operations. Basic calculations are addition/subtraction, multiplication/division, to more special-purpose operations such as squares, square roots, logarithms, and trigonometric functions.
[expandsub1 title=”Multipliers” expanded=”true”]
My focus has been on double floating-point numbers with 54-bit mantissa (including the assumed leading one). The area occupied by these multipliers dwarfs most other circuitry. Because of this, GPGPUs have trouble, including these high-precision multipliers. Tentatively, I believe my research will allow me to cut their size in half without losing any precision (no approximate computing).
[expandsub2 title=”Square Composed Multiplier – %(%span style=’font-size:12px; color:red;’ %)%future work%(%/span%)%”]
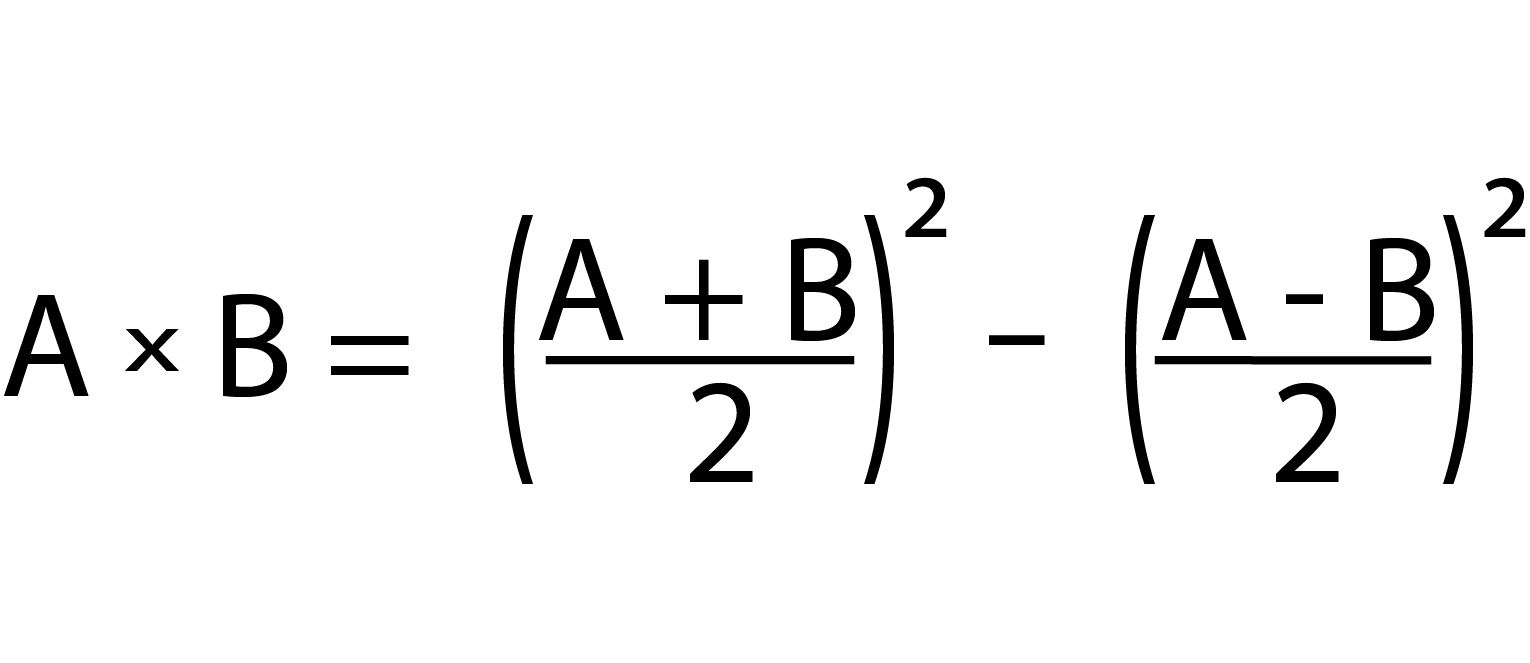
With my work in optimizing a square, my goal is to use the algebraic formula on the right to make an even smaller multiplier. Initial rough estimates indicate that, for a double-precision floating-point multiply, a reduction from 1,420 partial product additions down-to 1,020.
[/expandsub2]
[/expandsub1]
[expandsub1 title=”Squarers – %(%span style=’font-size:12px; color:red;’ %)%prior discovery%(%/span%)%”]
I have been working on squaring for a year and a half. It has come a long way with some major optimizations. This is my original paper, A Perspective into Squarer Optimization, submitted to the ARITH Symposium.
[/expandsub1]
[expandsub1 title=”Matrix Multiplication”]
[expandsub2 title=”Coppersmith-Winograd Algorithm”]
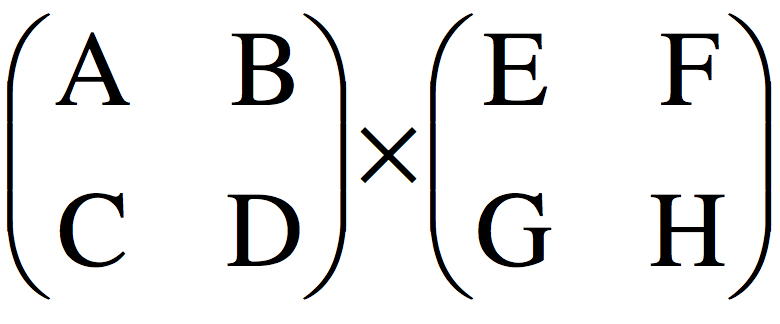 matrix multiplication. Due to this process’s efficiency, I often see algorithms with intensive squaring being expressed into matrices for multiplication. Would it be different if highly optimized squarers were native in traditional CPUs? Would algorithms be modified to use squarers over the multiple times slower multipliers? I was talking with Dr. George Constantinides of Imperial College of London, and on his website, he talks about Re-thinking Arithmetic. That term resonates with my curiosities. I envision that most mathematics is created utilization the tools of the period. With paradigm shifts in innovation, like highly efficient squarer or massively parallel computers, arithmetic processes may need re-thinking. I have definitively seen that to be the case as the highly computationally intensive Principal Components Analysis (PCA) has superseded Factor Analysis in reducing dimensionality.
matrix multiplication. Due to this process’s efficiency, I often see algorithms with intensive squaring being expressed into matrices for multiplication. Would it be different if highly optimized squarers were native in traditional CPUs? Would algorithms be modified to use squarers over the multiple times slower multipliers? I was talking with Dr. George Constantinides of Imperial College of London, and on his website, he talks about Re-thinking Arithmetic. That term resonates with my curiosities. I envision that most mathematics is created utilization the tools of the period. With paradigm shifts in innovation, like highly efficient squarer or massively parallel computers, arithmetic processes may need re-thinking. I have definitively seen that to be the case as the highly computationally intensive Principal Components Analysis (PCA) has superseded Factor Analysis in reducing dimensionality.[/expandsub2]
[expandsub2 title=”Tensors”]
 Understanding tensors are on my list of things I need to know. The TPU, the Tensor Processing Unit, is out there, and Coopersmith-Winograd’s algorithm uses tensors.
Understanding tensors are on my list of things I need to know. The TPU, the Tensor Processing Unit, is out there, and Coopersmith-Winograd’s algorithm uses tensors.[/expandsub2]
[/expandsub1]
[/expand]
[expand title=”Network-on-Chips (NoCs)”] 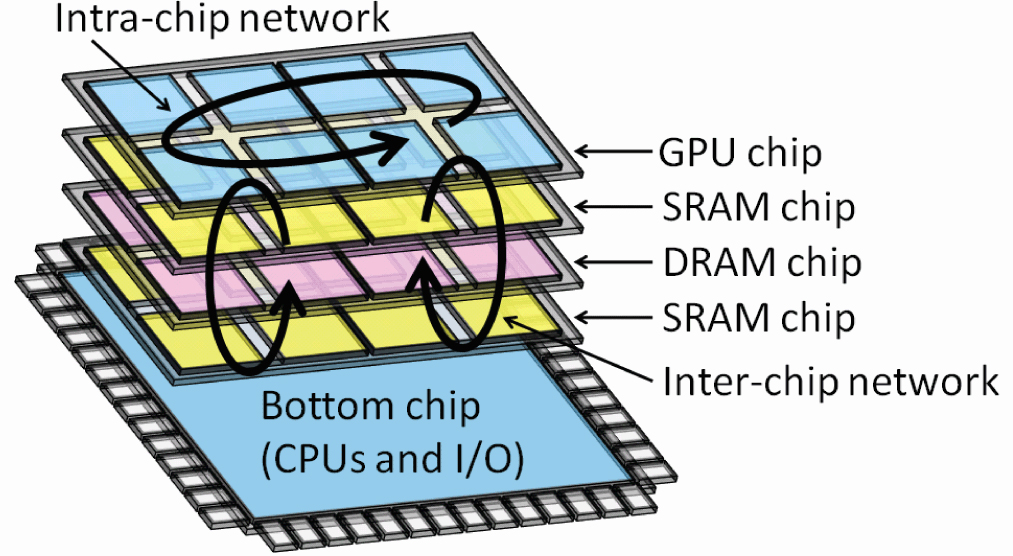
[/expand]
[expand title=”Compression Hardware”]
 Domain-Specific Hardware Accelerators, Dr. William Dally of Nvidia and Dr. Song Han of MIT talked about the efficiencies of using special logic compression circuits in their designs. Dr. Song was specifically discussing compression in Neural Networks and reducing the memory footprint, but it is also applicable to reducing bandwidth in NoCs.
Domain-Specific Hardware Accelerators, Dr. William Dally of Nvidia and Dr. Song Han of MIT talked about the efficiencies of using special logic compression circuits in their designs. Dr. Song was specifically discussing compression in Neural Networks and reducing the memory footprint, but it is also applicable to reducing bandwidth in NoCs.[/expand]
[expand title=”Asynchronous Computing”]
Asynchronous Computing has fascinated me for years.
The clock hand kept on ticking away and ignoring the figures which it approached, touched, left behind, and then again reached and again touched. It was absolutely indifferent to any goal, point, or segment.
– Thomas Mann
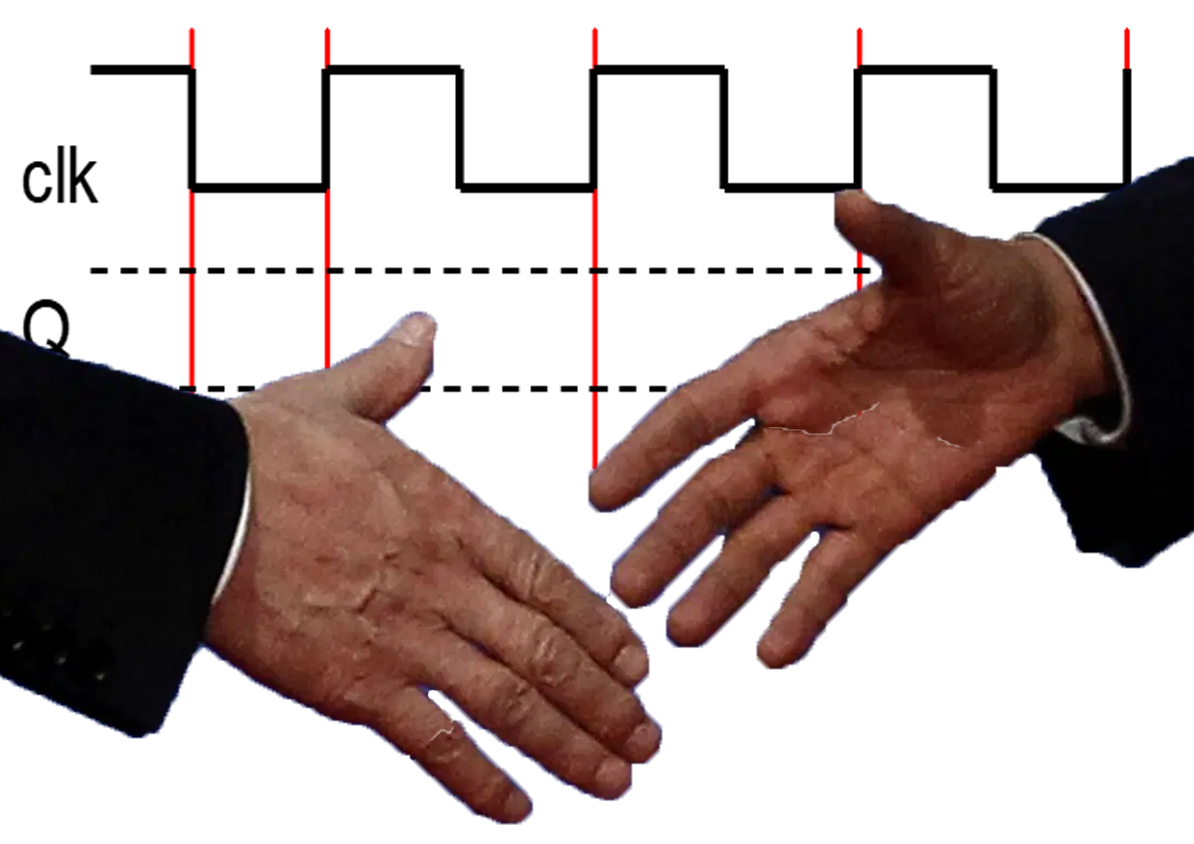 Clocked systems waste SO much time. A logic operation takes little time to compute waits on the same clock used by an adder or, worse, a multiplier. In reading research on asynchronous circuits, I commonly hear the authors question why this technology is not mainstream. I recently came across one of Prof. Mark Horowitz’s lectures that encouraged me that this technology had merit when he stated, “Why haven’t asynchronous circuits taken over the world? Because there is a lot of money being made with an entire CAD infrastructure behind synchronous design.”
Clocked systems waste SO much time. A logic operation takes little time to compute waits on the same clock used by an adder or, worse, a multiplier. In reading research on asynchronous circuits, I commonly hear the authors question why this technology is not mainstream. I recently came across one of Prof. Mark Horowitz’s lectures that encouraged me that this technology had merit when he stated, “Why haven’t asynchronous circuits taken over the world? Because there is a lot of money being made with an entire CAD infrastructure behind synchronous design.”
I see particular utilization within massively parallel computers where certain lengthy operations may vary in time. To me, it makes more sense to initiate the next data-independent process to be dispatched to a processor-based upon a handshake instead of a clock pulse.
[/expand]
[expand title=”Three-Dimensional Integrated Circuits”]
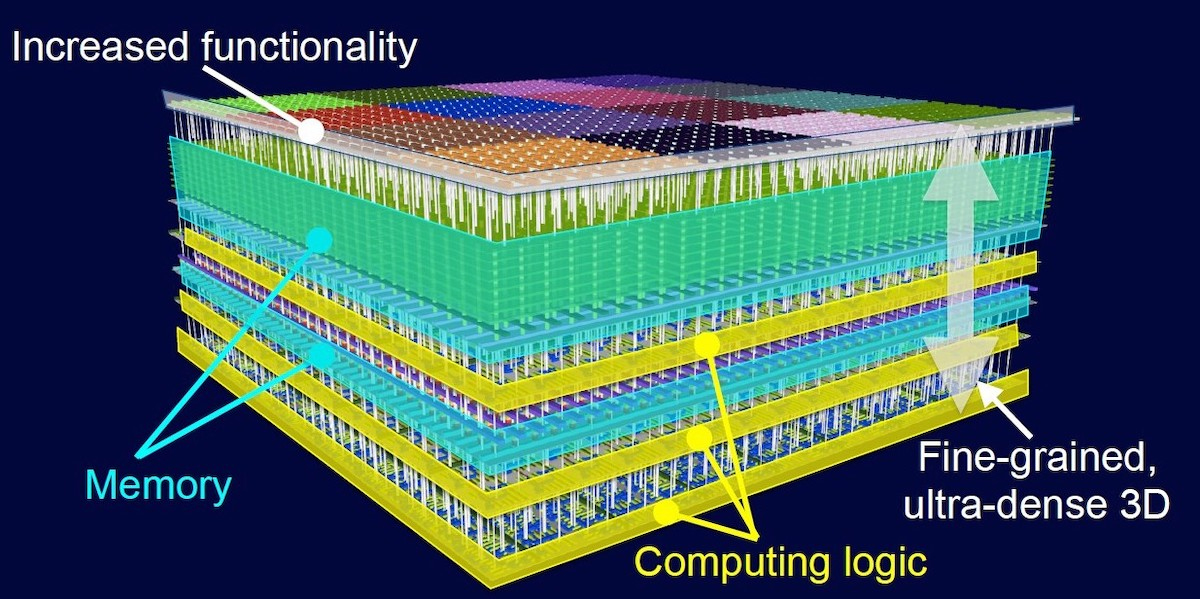 Just like how Asynchronous Computing makes all the sense in the world, so do Three-Dimensional Integrated Circuits(3D ICs). Just like cities, when you can’t grow out any further, you grow upwards. And with logic proximity being the major barrier to computational speed, it has to happen someday soon. My dad always tells me, “That a good college education will not train you for the technology of today, but will give you the foundations for the technology of tomorrow.” That is one reason I pursue classes in Physics, foreseeing the issues of technology like 3D ICs, where I will need to understand the physical underpinnings.
Just like how Asynchronous Computing makes all the sense in the world, so do Three-Dimensional Integrated Circuits(3D ICs). Just like cities, when you can’t grow out any further, you grow upwards. And with logic proximity being the major barrier to computational speed, it has to happen someday soon. My dad always tells me, “That a good college education will not train you for the technology of today, but will give you the foundations for the technology of tomorrow.” That is one reason I pursue classes in Physics, foreseeing the issues of technology like 3D ICs, where I will need to understand the physical underpinnings.
I was inspired by an article, An Overview of Thermal Challenges and Opportunities for Monolithic 3D ICs, where I became aware of the thermal ramifications (localized heat dissipation) of 3D ICs. The logic has to be laid out, so hot spots don’t occur. You don’t want a heavily used logic unit too close or on top of another. The current software will do layouts to prevent crosstalk between wires, memory, or logic, but taking into account heat dissipation seems too cool (or not). What a challenge! One, I wouldn’t mind getting my head around.
[/expand]
Areas of Knowledge Needing to Pursue:
Not only has my education been centrally focused on building Massively Parallel Computers, but I also recognize there are foundational educational topics that will support my research endeavors through the future. Technology changes, but most major developments require an understanding of physics to comprehend. It is my perspective that these subjects will provide me the tools I will need.
[expand title=”Condensate Physics”]
Solid foundations are not only today’s but also tomorrow’s technology. Most speed in computers is attributed to miniaturization. Transistors are so small they are being measured in the number of atoms wide. They’re not going to get much smaller. We are on the verge of a paradigm shift because our tried and true will not satisfy our needs for faster computers. It may be Quantum Computing, but we are still a long way from having enough qubits. Throughout the history of computers, the big advancements are born out of Physics. If I am going to comprehend future advancements, I must have a solid foundation in physics.
[/expand]
[expand title=”VLSI”]
In my one VLSI class at EPFL, the biggest impression I got was that the theory of Computational Arithmetic doesn’t allows follow reality. In our class, we competed to build the smallest and fastest 32-bit serial integer multiplier. Of course, my studies told me that a Booth Modified Radix-4 multiplier would do best. Surprise! That wasn’t the case. I did well, but other students beat my solution with simple, old fashion Ripple adders. The more I study, the more I realize I also need to know the underlining foundations.
[/expand]
[expand title=”GPU Architecture”]
[/expand]
[expand title=”NoC Design”]
NoCs are the backbone of successful massively parallel computers, and it is my quest to understand and develop a highly efficient network.
[/expand]
[expand title=”Logical Effort”]
[expandsub1 title=”Circuit Analysis in ‘C'”]
I need a better understanding of how to compute Logical Effort to analyze my circuits. Before building my circuits in VHDL, I always program them first in ‘C’. To test my idea, I go through all possible numbers to validate correct results. HDL simulators are slow, and it would take a long time to do this analysis. I would also like to be able to quickly modify my ‘C’ program circuitry to evaluate the impact of different configurations.
[/expandsub1]
[expandsub1 title=”FPGA Simulators Inconsistent”]
 I was asked to co-review a paper on cube-root calculations for IEEE Transactions on Computers. I am aware of the differences in FPGA architectures, but I came across a paper that was evidential in pointing out the fallacy in comparing statistics from different FPGA platforms. This paper showed up to a 230% difference in speed for identical algorithms on four different FPGAs. In my review, I pointed out the meaningless of making these comparisons. Not only I but the entire research community using FPGAs needs some tool to make an apples-to-apples comparison in terms of consistent measurements for the area (NAND gates not LUTs) and speed (Logical Effort).
I was asked to co-review a paper on cube-root calculations for IEEE Transactions on Computers. I am aware of the differences in FPGA architectures, but I came across a paper that was evidential in pointing out the fallacy in comparing statistics from different FPGA platforms. This paper showed up to a 230% difference in speed for identical algorithms on four different FPGAs. In my review, I pointed out the meaningless of making these comparisons. Not only I but the entire research community using FPGAs needs some tool to make an apples-to-apples comparison in terms of consistent measurements for the area (NAND gates not LUTs) and speed (Logical Effort).
[/expandsub1]
[expandsub1 title=”Wires? 70% of delay?”]
Third, Prof. Flynn proclaimed in ” ” that wires amount to 70% of the delay in a circuit. I am not sure that FPGA simulations are taking wire distances into account, and even if they were, their routing would be much different than ASICs or custom layout. And of course, as a high schooler, I don’t have access to Cadence or Synopsys software.
[/expandsub1]
[expandsub1 title=”Asynchronous Circuit Analysis”]
Fourth, Asynchronous circuits are my eventual goal. To build accurate handshaking circuits, I will need a tool that can provide a consistent measurement of propagation delay.
[/expandsub1]
[/expand]
[expand title=”Computer Architecture (more thorough understanding)”]
I have a pretty good familiarization with basic computer architecture, which was evident from succeeding in building a small CPU in VHDL. It was exciting to see it execute code, access a program and memory stack, and manipulate the FPGA LEDs. But, there is a lot more to real computers. They say you have begun to learn when you realize how much you don’t know. I know very little.
[/expand]
[expand title=”Chisel (greater expertise)”]
Just as people don’t program in assembler language anymore and instead use higher-level programming languages, people who architect computers don’t design computers at the transistor level; instead, they use the high-level language Chisel can put out computer designs so much faster.
[/expand]